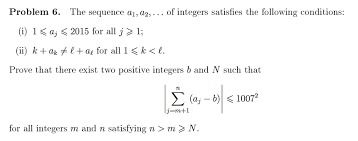Cuando estaba en la secundaria, mi maestra de matemáticas nos estaba enseñando sobre construcciones de regla y compás. ¿Todavía les enseñan esto a los niños? De todos modos, nos había enseñado cómo construir ciertas formas, luego nos informó: el heptágono, o polígono regular de siete lados, no se puede construir usando una regla y una brújula.
Mi maestra estaba desconcertada. Sabía que el heptágono no se podía dibujar con estas herramientas de dibujo, pero allí estaba frente a sus ojos.
Si no puede ver el video, estos son los pasos:
- Primero, dibuja un círculo, centro A, y elige un punto B en el círculo.
- Dibuja otro círculo con el mismo radio, centrado en B esta vez.
- Los dos círculos se encuentran en dos puntos, C y D.
- Encuentre el lugar donde se encuentran AB y CD, y llámelo E.
- Luego, configura tu brújula en CE. Esa distancia funcionará perfectamente como la longitud del borde de un heptágono.
La razón por la que esto funciona es que la distancia entre C y E (en relación con AB) resulta ser la mitad de la raíz cuadrada de tres, o aproximadamente 0,866025. La longitud correcta necesaria para dibujar un heptágono es 0.867767. Estos números están tan juntos que necesitarías una habilidad increíble (un lápiz muy afilado) para notar la diferencia. Si su círculo mide 6 pulgadas de ancho, la longitud CE está mal en menos de un séptimo de milímetro, aproximadamente una parte en 192 de una pulgada.
Cuando las personas dicen que algo puede o no construirse con una regla y una brújula, quieren decir exactamente, utilizando un hipotético lápiz infinitamente afilado y un dibujante perfectamente capacitado. En la vida real, puede acercarse lo más que quiera a cualquier forma que desee.
Pasaron muchos siglos antes de que las personas supieran cómo demostrar que un heptágono no era construible. La idea clave vino de un joven llamado Évariste Galois. Era un genio matemático increíble, que tristemente se involucró en la política francesa a principios del siglo XIX. Sus enemigos lo desafiaron a un duelo, y le dispararon fatalmente a la edad de 20 años. La noche anterior al duelo se lo pasó escribiendo a amigos, y también escribiendo la mayor cantidad posible de matemáticas, para que no se perdiera en el mundo si perdió el duelo. Más tarde, los matemáticos que trabajaron en sus trabajos encontraron la marca del genio. Todo un campo de las matemáticas lleva el nombre de este hombre que murió demasiado joven.
La moraleja de la historia? No te involucres en la política de principios del siglo XIX: las matemáticas son más importantes.
Si usa una regla y una brújula para construir un nuevo punto a partir de algunos existentes, habrá una ecuación cuadrática que satisfaga las coordenadas del nuevo punto. Los coeficientes de la cuadrática se derivan de las coordenadas de los puntos que ya tenía. La teoría de Galis muestra que, de hecho, puede encontrar un polinomio con coeficientes de números enteros para las coordenadas del nuevo punto. El grado de este polinomio será una potencia de dos.
Entonces, ¿qué pasa con el heptágono? Tiene un punto cuyas coordenadas son el seno y el coseno de 360/7 grados. Si x es este coseno, satisface una ecuación cúbica 8x3+ 4x2-4x-1. Esto no tiene un grado 2, 4 u 8, ni ninguna potencia de dos, por lo que el heptágono no se puede construir con una regla y una brújula.
¡Y ahí lo tienes!