Sugerencias para sumar (y restar) fracciones
La forma «estándar» de sumar (o restar) fracciones es colocarlas primero sobre un denominador común. Entonces, el problema de la fracción


es
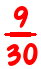

A menudo, los denominadores no tienen un factor común (excepto 1), por lo que colocar las fracciones sobre un denominador común significa multiplicar la parte superior e inferior de cada fracción por el denominador de la otra.


es
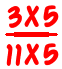

Esta es una regla más simple de recordar, y también funciona cuando los denominadores tienen un factor común.


es
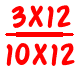
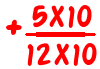
Así que es un buen método para usar, y (creo) que los niños a menudo descubrirán este método más simple y lo usarán a favor del método «estándar» de encontrar primero el «mejor» común denominador. Sé que mi hijo lo hizo. Sin embargo, este método causa problemas cuando los denominadores tienen un gran factor común.
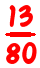

es
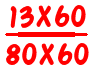
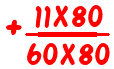
que es muy dificil Bueno, más difícil de lo que debe ser. Después de todo, ¿quién quiere hacer ejercicio 80 x 60 o 11 × 80 + 13 × 60 cuando en realidad no lo necesitan?
Si conoce a alguien que usa este método (y a veces obtiene grandes números para multiplicar), entonces hay buenas noticias. Todavía pueden usar su método, con solo un pequeño ajuste, no habrá más multiplicación de números grandes a menos que sea absolutamente necesario.
La clave es que 60 y 80 tienen un múltiplo común bajo, es decir 240. Ahora, 240 = 4 × 60 y 240 = 3 × 80. Llamemos a los números 4 y 3 el cofactores de 60 y 80. ¿Por qué? Cofactores? Debido a que 60 x 4 = 240, 4 y 60 van juntos como factores de 240. Del mismo modo, 3 y 80 son factores «juntos» de 240. Debido a que 3 va «juntos» con 80 en algún sentido, cofactor Es un buen nombre.
{Rompecabezas: ¿puedes encontrar un número y un factor de ese número que es su propio cofactor}
Ahora, volviendo a la pregunta de suma de fracciones. Hacer ejercicio
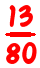

No tenemos que multiplicar 80 por 60, o 60 por 80, solo tenemos que multiplicar 80 por su cofactor (3) y 60 por su cofactor (4). Entonces obtenemos
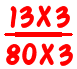

Multiplicar la parte superior e inferior de cada fracción por un cofactor del denominador hará que los denominadores de las dos fracciones sean iguales. Entonces, modificando ligeramente el método (cambiando «multiplicar por el denominador de la otra fracción» a «multiplicar por el cofactor de esta fracción») regresa al método «estándar», sin la necesidad de cambiar completamente el pensamiento del estudiante.
Si la palabra «cofactor» es confusa, no se moleste con ella. Lo usé porque «el cofactor de 60» es más corto que «el número por el que multiplicas 60 para obtener el mínimo común múltiplo que has notado que tiene 60 y 80».
En realidad, no tiene que encontrar el mínimo común múltiplo para que este método funcione. Si encontrara el múltiplo común 480 en lugar de 240, los cofactores de 60 y 80 serían 8 y 6, y la suma de fracciones sería


Los números involucrados se hacen un poco más grandes y hay un poco más de simplificación al final, pero aún así obtendrá la respuesta correcta sin demasiados problemas.







